Teorem ve problemlerden bazıları çıktıkları dönemlerden günümüze kadar hala cevaplanması bekleyen sorular arasında yer alabiliyor. Bunlarda biri de Collatz Sanısı. Alman matematikçi Collatz’ın matematik problemi kısacık soruda uzun hesaplamalar gerektiren, basit görünen ama son derece zor bir denklemdi. 

LOTHAR COLLATZ’IN KISA DENKLEMİ NE?

Takvimler 1910 yılının 6 Temmuz gününü gösteriyordu. Gelecekte dünya çapında çözümü bir sır olacak problemin kâşifi hayata gözlerini açtı. Lothar Collatz pek çok Alman genci gibi eğitimini de çok farklı okullarda bulunmuş ve başarıyla tamamladı. Onun için en önemli ders ise severek çalıştığı matematik olmuştu. Hatta ilerleyen yaşlarında ona pek çok ödül kazandıran ve adını dünya çapında duyuran da yine kariyerine ve 80 yıllık yaşamına damga vuran matematik oldu. Collatz henüz 27 yaşındayken sorduğu bir sorunun çözümü ise onlarca matematikçinin günlerce, aylarca düşünmesine sebep oldu. Adına ‘Collatz Sanısı’ denen bu problem 1937’den bugüne çözülemeyen bir sır olarak kalmıştı. Çözülemeyen pek çok matematik problemi olmasına rağmen Collatz’ınki kısacık soruda uzun hesaplamalar gerektiren, basit görünen ama son derece zor bir denklemdi.

Lothar Collatz, 1928'de Greifswald Üniversitesi'ne girdi, Münih’e, ardından Göttingen'e ve son olarak Berlin'e giderek burada Alfred Klose'un yanında doktora eğitimi aldı. Collatz, 1935 yılında, 25 yaşındayken “Doğrusal diferansiyel denklemler için daha yüksek yaklaşıma sahip fark yöntemi” adlı teziyle doktora unvanını aldı. 1937’de ise o meşhur soruyu sordu: ‘3 x 1.’  Lothar Collatz, sayısal analiz üzerinde belki de en çok çalışan bir Alman matematikçiydi.

DÖNEMİN POPÜLER MATEMATİKÇİLERİ ONDAN İLHAM ALDI

Lothar Collatz konuşmalarında ve katıldığı konferanslarda sık sık Hilbert, Courant, Richard von Mises, Schur ve o dönemin diğer ünlü matematikçilerinin derslerinden ne kadar etkilendiğini anlatıyordu. Matematiğin ve matematikçilerin, hesaplamalarının sonuçlarını gerçek dünya şartlarında uygulama ve onlar tarafından motive edilme sorumluluğu olduğuna inanıyordu. Collatz hayatının hiçbir evresinde bu inancı uğruna savaşmaktan da asla yorulmadı. Etkilendiği isimler arasında yer alan Richard von Mises ve Collatz arasında ise özel bir bağ vardı. Lothar Collatz, Macar matematik profesörü Alfred Klose'un doktora öğrencilerinden biriydi. Ancak Richard von Mises'in Klose’un altında çalışmalarını tamamlayan son öğrencisi oldu ve 1933'te devlet sınavını özel olarak geçmeyi Collatz’dan önce başardı. İkili arasında hem etkileyici bir matematik fırtınası hem de dostça bir yarış vardı. Collatz’ın ismi ise on yıllarca bambaşka yerlerde matematik seven herkesin bildiği gizemli problemi sayesinde hiç unutulmadı. Hatta dünyaca ünlü matematikçiler dahi günümüzde kullanılan matematiğin Collatz Sanısı için yetersiz olduğunu söylüyordu.

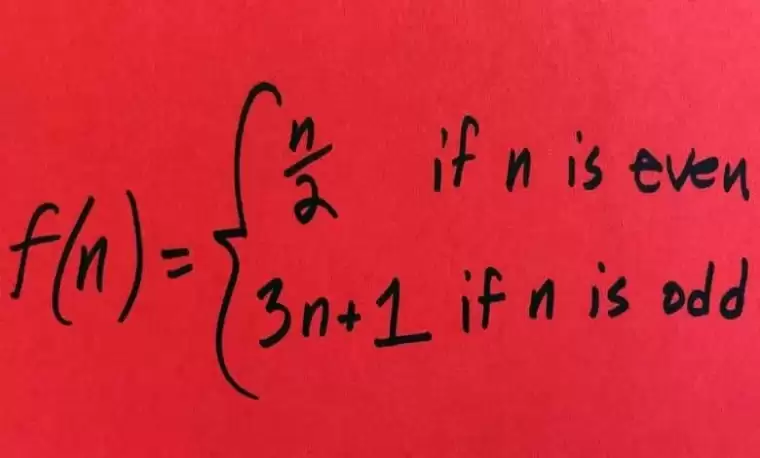
BU PROBLEM 87 YILDIR NEDEN ÇÖZÜLEMEDİ?

Yapılan analizler sonucunda bulmacanın sadece sayı teorisiyle değil, kaos teorisi ve hesaplamanın temelleri gibi alanlarla da bağlantısının olduğu ortaya çıkıyordu. Yani bu sorunun tek bir sonucu da olsa, sonuca giden yolda ve sonuçtan sonra gidilecek pek çok sapak vardı. Matematiğin kilit noktalarından birinde Lothar Collatz’ın kısa ama kritik problemi duruyordu. Matematikçiler, mevcut matematik anlayışı ve araçlarının bu tahmini çözmek için yetersiz kalabileceğini belirtiyordu. Bu yüzden bu işlemlere çok fazla kaynak ayırmanın potansiyel olarak aşırı zaman kaybına yol açabileceğini düşünüyorlardı. Neredeyse 100 yıl önce ortaya atılan soruya vakit ayıranlar vardı elbette. Paul Erdős’un, Collatz varsayımı hakkında söyledikleri de pek çok matematikçinin ifade etmek istediğiydi. "Matematik bu tür problemlere hazır olmayabilir" diyordu Erdős.

Collatz Sanısı’nın ilk ortaya çıktığı günden 73 yıl sonra Jeffrey Lagarias, "Günümüz matematiğinin tamamen ulaşamayacağı olağanüstü derecede zor bir problem olduğu" kararına vardı. Lagarias ayrıca Collatz varsayımı yapan ve pek çok makale yazan nadir matematikçilerden biriydi. Belki de Collatz Sanısı’nın bulunamayan cevabı birilerinin ona ayırmadığı zamanda saklıdır. Collatz Sanısı çözüldüğü takdirde, hem basit bir eğitim aracı olarak hem de derin matematiksel soruları keşfetmek için bir kapı işlevi görebilir.